Understanding the Fundamental Concept of Multiplication
The process of multiplying numbers is a cornerstone of mathematics. It represents repeated addition and is fundamental to numerous applications, from basic calculations to advanced scientific computations. Multiplication simplifies the process of adding the same number multiple times, significantly increasing efficiency and accuracy. For example, calculating the total cost of 5 identical items at a certain price is much faster using multiplication than summing the price five times.
Multiplication's importance transcends the realm of basic arithmetic. It plays a critical role in various mathematical disciplines, including algebra, geometry, and calculus. Its principles underpin algorithms and computations in many scientific fields, from engineering and physics to computer science. Historically, the development of efficient multiplication methods has been a driving force in technological advancements and broader societal progress. Different systems for multiplication have emerged across cultures, reflecting the diversity of mathematical thought and development.
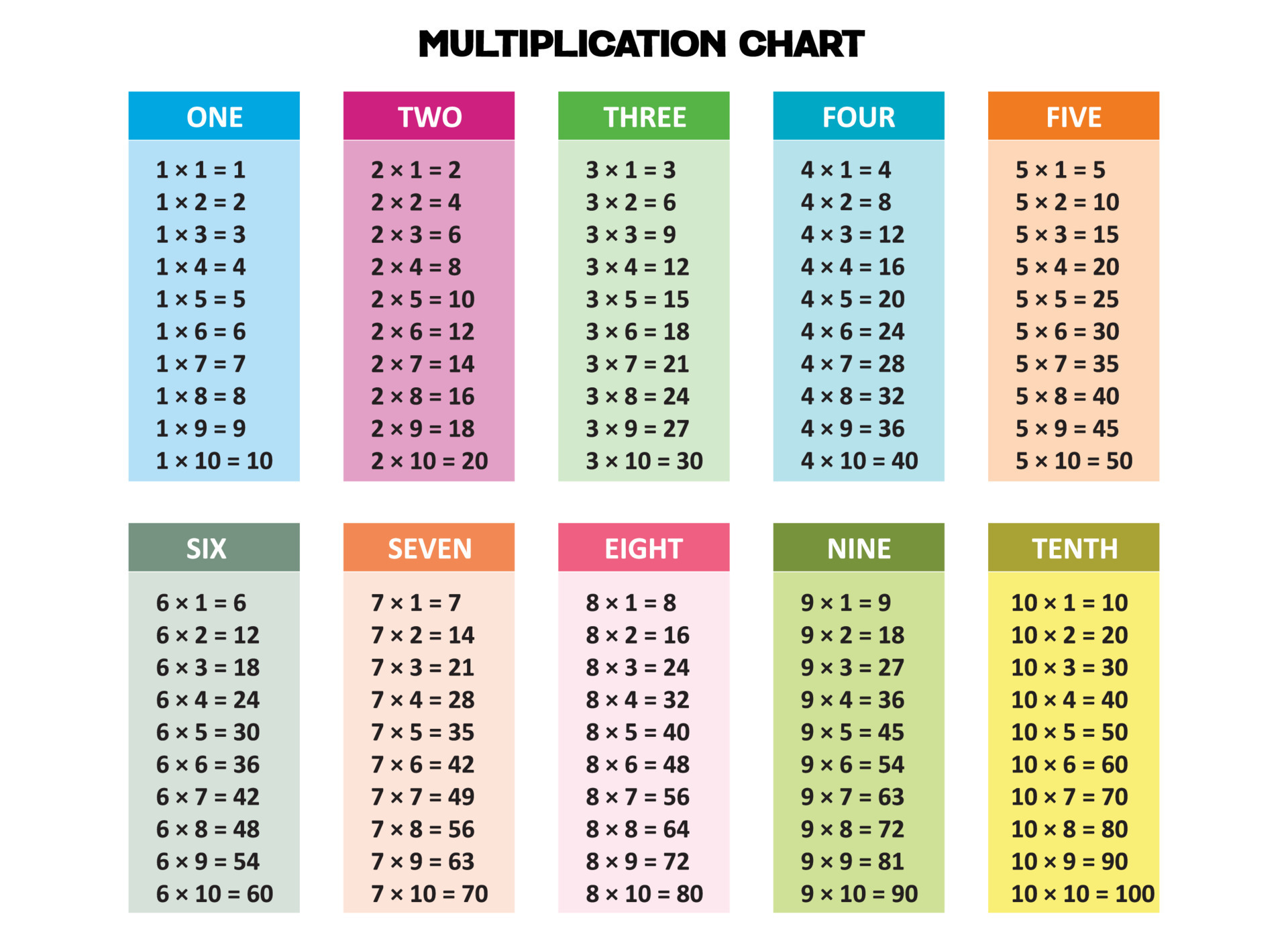
Multiplication
Multiplication is a fundamental arithmetic operation. Its core principles underpin numerous mathematical concepts and applications.
- Repeated addition
- Number scaling
- Area calculation
- Factorization
- Distributive property
- Commutative property
- Associative property
- Order of operations
These aspects demonstrate the interconnectedness of multiplication with other mathematical concepts. Repeated addition, for instance, forms the basis of multiplication, illustrating how a series of the same addition can be concisely represented through multiplication. Area calculation directly utilizes multiplication to find the area of a rectangle; the length multiplied by the width. Factorization, meanwhile, employs multiplication to decompose numbers into their factors. The properties of commutativity, associativity, and the distributive property underpin algebraic manipulation and problem-solving.
1. Repeated Addition
Repeated addition forms the conceptual foundation of multiplication. The essence of multiplication lies in the concise representation of repeated addition. Consider the problem of calculating the total cost of five identical items priced at $3 each. Directly adding $3 five times yields the total. Multiplication, however, offers a more efficient means of achieving the same result: 5 multiplied by 3. This simplification highlights multiplication's inherent efficiency over repeated addition, especially when dealing with a larger number of repetitions.
The practical significance of understanding this connection is profound. It allows for a transition from rudimentary calculation to more complex mathematical operations. This foundational understanding of repeated addition enables the manipulation of numerical expressions in algebraic contexts. Furthermore, understanding that multiplication is essentially a shorthand for repeated addition clarifies how this fundamental operation underpins more advanced mathematical concepts, including those utilized in geometry, calculus, and beyond. By recognizing multiplication's relationship to repeated addition, one gains a deeper appreciation for its power and widespread applicability. In essence, this connection is critical for the advancement of mathematical knowledge.
In summary, repeated addition serves as the conceptual building block for multiplication. The ability to recognize multiplication as a concise representation of repeated addition facilitates a deeper understanding of the operation itself and allows for the application of these principles to a broader range of mathematical problems, from basic arithmetic to complex calculations used across various disciplines.
2. Number scaling
Number scaling, a critical aspect of mathematical operations, directly correlates with multiplication. Scaling involves increasing or decreasing a quantity by a specific factor. Multiplication serves as the primary mechanism for this scaling process. When a number is multiplied by a factor greater than 1, its value increases proportionally. Conversely, multiplying by a factor between 0 and 1 results in a decrease. This relationship is fundamental, allowing for the efficient representation and manipulation of numerical quantities across diverse mathematical applications.
Consider a simple example: calculating the price of 10 identical items, each priced at $5. To determine the total cost, one multiplies the price of a single item ($5) by the quantity (10). This multiplication directly scales the price of one item to encompass the total cost of 10 items. Similarly, in engineering, scaling blueprints of structures involves multiplying the dimensions of the original design by a scaling factor to achieve the desired final size. This scaling process employs multiplication as its core operation. In financial modeling, scaling investment portfolios to accommodate growth projections often utilizes multiplication. These examples illustrate how multiplication underpins the process of scaling, enabling the practical application of mathematical principles in diverse real-world scenarios.
Understanding the connection between number scaling and multiplication is crucial for comprehending fundamental mathematical concepts and their applications. This knowledge allows for accurate and efficient calculations in various fields, including engineering, finance, and everyday problem-solving. The ability to scale quantities using multiplication underpins the efficiency and accuracy of many mathematical processes. This principle is a cornerstone for further explorations into more advanced mathematical concepts and applications.
3. Area Calculation
Determining the area of a two-dimensional shape is fundamentally linked to multiplication. The relationship is inherent and crucial for understanding the spatial characteristics of various geometric figures.
- Rectangles and Parallelograms
The area of a rectangle is calculated by multiplying its length and width. This straightforward formula is directly derived from the concept of multiplication as repeated addition. Imagine a rectangle divided into smaller squares; the number of squares along the length multiplied by the number along the width represents the total area, mirroring the essence of multiplication. This principle applies equally to parallelograms, which can be viewed as a modified rectangle. Real-world applications are countless, from calculating the floor space of a room to determining the surface area of a wall.
- Triangles
Triangles share a crucial connection to multiplication. The area of a triangle is half the product of its base and height. This relationship highlights the connection between multiplication and the geometric properties of different shapes. Visualize a rectangle encompassing two identical triangles; the area of one triangle is precisely half the area of the encompassing rectangle, demonstrating the proportional relationship between multiplication and area in various geometric figures. Applications range from surveying land areas to engineering design.
- Circles
Circles involve a more sophisticated application of multiplication. The area of a circle is calculated by multiplying (pi) by the square of its radius. This formula, while seemingly distinct, utilizes the multiplicative property of to accurately determine the area enclosed within the circular boundary. Applications include calculating the area of circular plots of land, the cross-sectional area of pipes, and various engineering calculations requiring the area of circular shapes.
- Complex Shapes
More complex shapes can often be subdivided into simpler geometric figures. By calculating the area of each component and summing the results, multiplication plays a vital role in determining the overall area of such intricate forms. This principle is critical for architectural design, engineering planning, and various analytical processes. In essence, the fundamental principle of multiplication simplifies the determination of area for intricate shapes.
Across diverse geometric shapes, multiplication serves as the unifying mathematical tool for computing area. From the basic rectangle to intricate figures, the multiplicative principle consistently dictates the computation of area. This connection highlights the fundamental role of multiplication in geometric measurement and its applications in real-world scenarios and complex mathematical analyses.
4. Factorization
Factorization, a crucial process in mathematics, involves decomposing a number or expression into its constituent factors. This decomposition is fundamentally linked to multiplication, as the factors, when multiplied together, yield the original number or expression. The understanding of factorization is essential for simplifying mathematical expressions, solving equations, and comprehending the inherent structure of numbers.
- Prime Factorization
Prime factorization breaks down a number into its prime factors. These prime factors are whole numbers greater than 1 that are only divisible by 1 and themselves. For example, the prime factorization of 12 is 2 x 2 x 3. Prime factorization is pivotal in numerous mathematical applications, from cryptography to number theory. The unique prime factorization of any integer is a fundamental theorem underpinning many algorithms.
- Common Factors
Identifying common factors is a significant application of factorization. Common factors are shared divisors of two or more numbers. Understanding these common factors enables simplification of fractions and expressions. For instance, the fraction 12/18 can be simplified to 2/3 by dividing both numerator and denominator by their greatest common factor, 6. This reduction streamlines calculations and clarifies the essential relationship between the numbers.
- Applications in Solving Equations
Factorization proves vital for solving various equations. By factoring an equation, one can often simplify it into a more manageable form, potentially isolating variables to solve for them. Consider the quadratic equation x - 5x + 6 = 0. Factoring the quadratic expression as (x - 2)(x - 3) = 0 leads directly to the solutions x = 2 and x = 3. This application highlights factorization's role in making complex problems more approachable and solvable.
- Polynomial Factorization
Factorization extends to polynomials, expressions involving variables and exponents. Methods like grouping and the quadratic formula play important roles in breaking down complex polynomial expressions into simpler components. This process significantly simplifies algebraic manipulations and has applications in areas like engineering and physics, where polynomial equations describe numerous physical phenomena.
In summary, factorization is an indispensable tool in mathematics, tightly interwoven with the concept of multiplication. Its diverse applications, from prime factorization and common factors to solving equations and working with polynomials, demonstrate the practical significance and underlying structure of numbers. This understanding is crucial for progressing beyond basic arithmetic and tackling more intricate mathematical problems and their related applications.
5. Distributive Property
The distributive property establishes a crucial connection between multiplication and addition. It dictates how multiplication interacts with sums and differences, offering a powerful tool for simplifying expressions and solving mathematical problems. This property is fundamental to numerous algebraic manipulations and plays a significant role in diverse mathematical applications. Its direct relevance to the process of multiplication underpins its importance.
- Fundamental Principle
The distributive property asserts that multiplying a number by a sum or difference yields the same result as multiplying the number by each term of the sum or difference and then adding or subtracting the products. This principle is expressed as a (b + c) = (a b) + (a c) and a (b - c) = (a b) - (a c). These equations encapsulate the essence of the property, showcasing its ability to distribute multiplication across addition and subtraction.
- Simplification of Expressions
The distributive property is instrumental in simplifying complex algebraic expressions. By applying the property, often a significant reduction in the number of terms is achieved. This process makes expressions more manageable for further analysis and problem-solving. For instance, 3 (x + 5) can be transformed to 3x + 15, clarifying the relationship between the variable and the constant terms. This simplification enables further algebraic manipulation and solutions.
- Solving Equations
The distributive property is frequently employed in equation solving. Expanding expressions using the distributive property often leads to the isolation of variables for subsequent solution. This strategic application of the property allows for the rearrangement of terms in an equation to isolate the unknown variables. Consider the equation 2 (y - 4) = 10; applying the distributive property yields 2y - 8 = 10. This transformed expression facilitates the isolation and calculation of the value for y.
- Real-world Applications
The distributive property is not limited to abstract mathematical concepts. Calculating the total cost of multiple items with varying prices directly utilizes this principle. If a set of items, some costing $10 and others $15, are purchased, multiplying each price by the corresponding quantity and summing the results is identical to applying the distributive property to ascertain the total cost. Similar applications exist in engineering, finance, and other fields.
In essence, the distributive property is an integral part of the multiplication process. By simplifying expressions and facilitating equation solutions, it directly contributes to mathematical efficiency and clarity. The ability to distribute multiplication across addition and subtraction, as dictated by the distributive property, significantly impacts the application of multiplication to broader mathematical contexts.
6. Commutative Property
The commutative property of multiplication asserts that the order of factors does not affect the product. This fundamental principle is intrinsically linked to the nature of multiplication, significantly impacting its application in various mathematical contexts. Understanding this property simplifies calculations and clarifies the inherent structure of multiplication. Its relationship to multiplication is direct, illustrating that the arrangement of numbers being multiplied doesn't alter the final outcome.
- Order Independence
The core concept is that changing the order of the numbers being multiplied does not change the result. For example, 2 3 yields the same product as 3 2. This order independence simplifies calculations by allowing flexibility in arranging factors. This applies regardless of the specific numbers involved, ensuring consistency in the outcome, irrespective of the order in which numbers are multiplied.
- Applications in Multiplication
The commutative property streamlines calculations by allowing for the rearrangement of factors to obtain simpler products. This is particularly useful when dealing with larger numbers or complex expressions. In the realm of practical applications, ordering factors strategically facilitates easier computation. For instance, calculating the cost of 5 items priced at $2 each is easily calculated as 5 2 or 2 5, both yielding the same result.
- Simplification of Expressions
The commutative property's application extends to more complex expressions. Rearranging terms involving multiplication can often lead to simplified products or expressions. This is relevant in algebraic equations and expressions, facilitating simplification and clarity.
- Relationship to Other Properties
The commutative property interplays with other mathematical properties like associativity. While commutativity focuses on order within a multiplication, associativity addresses the grouping of factors within a sequence of multiplications. These principles in conjunction allow flexibility in ordering and grouping factors, greatly influencing how multiplication expressions are evaluated and manipulated.
In conclusion, the commutative property of multiplication is a fundamental concept, simplifying calculations and elucidating the essence of multiplication itself. Its order independence, direct applicability in various contexts, and relationship with other properties further highlights its significance in the broader landscape of mathematics. This propertys impact on practical computations and symbolic manipulations solidifies its importance to multiplication.
7. Associative Property
The associative property of multiplication dictates how grouping factors within a sequence of multiplications affects the final product. Crucially, the grouping of factors, not the order, is the key element. This property is inherent to multiplication's fundamental operation and significantly impacts problem-solving strategies across diverse mathematical applications.
The core principle is that the grouping of factors in a multiplication sequence does not alter the resultant product. For example, (2 x 3) x 4 equals 2 x (3 x 4). Both expressions yield 24. This invariance in the product, despite regrouping, illustrates the associative property's consistency. This fundamental principle, while seemingly simple, underpins the efficiency and validity of many mathematical computations, facilitating strategic ordering and grouping choices.
The practical significance of this understanding extends beyond basic arithmetic. Consider evaluating the total cost of multiple items with varying quantities and prices. If a retailer sells different-priced items in bulk, the associative property allows flexibility in calculating the total cost by regrouping the numbers and using the most convenient calculations. In more complex scenarios, such as calculating the volume of a rectangular prism, the property allows one to select the most advantageous order of operations for numerical efficiency. This property's utility encompasses a range of real-world applications, highlighting its critical role in mathematical problem-solving.
In summary, the associative property of multiplication ensures consistency in the product regardless of the grouping of factors in a multiplication sequence. This property's practical implications extend from simplifying arithmetic calculations to tackling more intricate mathematical problems, showcasing its inherent value and significance within the broader context of mathematical operations.
8. Order of Operations
The order of operations, a fundamental principle in arithmetic and algebra, dictates the specific sequence for evaluating expressions involving multiple operations. This sequence is crucial, particularly when multiplication is involved, ensuring consistent and accurate results. Without a standardized order, ambiguity arises, leading to varied interpretations and incorrect solutions. This principle is paramount in preventing misunderstandings and fostering a unified approach to mathematical calculations.
Multiplication, as a fundamental arithmetic operation, is directly impacted by the order of operations. Consider an expression like 2 + 3 x 4. Without a defined order, there's potential for two distinct interpretations. Following the established order of operationsfirst performing multiplication, then additionyields 2 + (3 x 4) = 2 + 12 = 14. If addition were performed before multiplication, the result would be (2 + 3) x 4 = 5 x 4 = 20. The stark difference underscores the necessity of a predefined order. This principle ensures consistent interpretation and avoids contradictory results in complex calculations. Real-world examples range from calculating compound interest to engineering designs, where precise mathematical procedures are essential. In essence, the order of operations prevents ambiguity, promoting clarity and accuracy.
The importance of understanding the order of operations extends beyond simple calculations. In advanced mathematics and scientific applications, where complex equations involve multiple operations, adhering to the order of operations is critical. Errors in calculation due to ambiguous procedures can have significant ramifications, ranging from inaccuracies in scientific experiments to financial discrepancies in accounting. Therefore, the proper application of the order of operationsincluding multiplicationis not just an academic exercise; it underpins the very foundation of numerous practical applications.
Frequently Asked Questions about Multiplication
This section addresses common queries related to the fundamental mathematical operation of multiplication. Clear and concise answers are provided to promote a deeper understanding of this critical skill.
Question 1: What is the core concept behind multiplication?
Multiplication represents repeated addition. Instead of adding the same number repeatedly, multiplication provides a shorthand method for calculating the total when a quantity is added a specific number of times. For example, 3 multiplied by 4 is equivalent to adding 3 four times (3 + 3 + 3 + 3).
Question 2: How does multiplication differ from division?
Multiplication involves combining equal groups of numbers. Division, conversely, involves separating a quantity into equal groups. While they operate on different principles, understanding the inverse relationship between multiplication and division is essential for performing calculations correctly.
Question 3: What are the basic properties of multiplication?
Key properties include the commutative property (order of factors doesn't affect the product), the associative property (grouping of factors doesn't affect the product), and the distributive property (multiplying a number by a sum is equivalent to multiplying the number by each addend and summing the results). Understanding these properties simplifies complex calculations.
Question 4: How is multiplication applied in real-world situations?
Multiplication has diverse applications in everyday life, such as calculating costs for multiple items, determining areas of shapes, and analyzing data in various fields. Its utility extends from basic calculations to complex scientific and financial computations.
Question 5: What is the importance of mastering multiplication?
Mastering multiplication is foundational for progressing to more advanced mathematical concepts. It lays the groundwork for success in algebra, geometry, and higher-level mathematics, which often depend upon an understanding of multiplication's fundamental principles. Improved calculation speed and accuracy are secondary benefits of understanding multiplication.
A strong grasp of multiplication principles is essential for success in mathematics and many real-world applications. Understanding the core concepts and properties of multiplication is fundamental for advancing in mathematics and beyond.
Next, we will delve into the practical application of multiplication through problem-solving examples.
Conclusion
This exploration of multiplication underscores its fundamental role in mathematics. From the basic concept of repeated addition to the sophisticated application in geometry and algebra, multiplication underpins numerous mathematical operations and real-world applications. Key properties, such as commutativity, associativity, and distributivity, simplify complex calculations and reveal the inherent structure of numbers. The importance of understanding these properties extends far beyond basic arithmetic, influencing problem-solving in diverse fields, from engineering to finance.
Mastering multiplication is not merely a stepping stone; it's a cornerstone for future mathematical endeavors. A solid foundation in multiplication principles enables the efficient and accurate resolution of increasingly complex problems. A profound understanding of this fundamental operation lays the groundwork for tackling more intricate mathematical concepts and fosters a deeper appreciation for the logical structure inherent in mathematics. Continued study and practice solidify this foundational knowledge, opening doors to further exploration within the broader realm of mathematics.

Detail Author:
- Name : Stephen Schumm
- Username : florian73
- Email : wilburn07@wyman.info
- Birthdate : 1984-06-24
- Address : 975 Jameson Circle South Onaville, IL 50446-5363
- Phone : 424.330.4498
- Company : Cartwright Group
- Job : Agricultural Inspector
- Bio : Ad tempore sunt magnam blanditiis qui fugiat. Voluptatem dolorem ut voluptatibus consequatur. Error laboriosam nesciunt optio velit animi qui.
Socials
twitter:
- url : https://twitter.com/stacey.larkin
- username : stacey.larkin
- bio : Iure nihil aspernatur et autem dolorum aut et. Quis qui saepe quae voluptatum qui eos. Consectetur quia soluta error cum tempore sapiente autem.
- followers : 5894
- following : 122
facebook:
- url : https://facebook.com/larkins
- username : larkins
- bio : Aut ipsa quidem libero doloribus. Sit qui enim dolor debitis quas sequi.
- followers : 4783
- following : 1995